Kissen-Platte

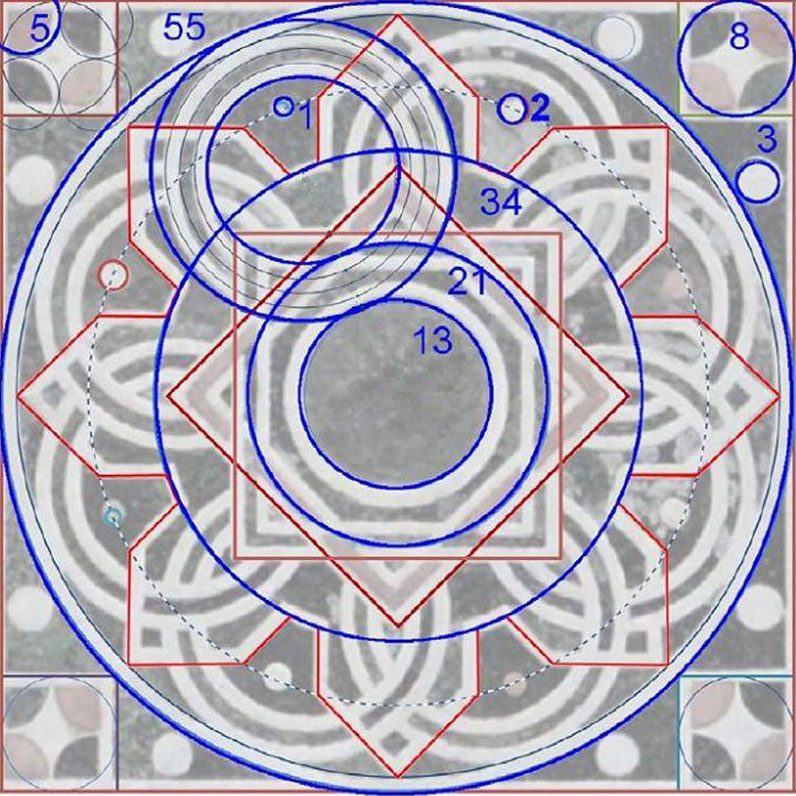
Der italienische Rechenmeister Leonardo Fibonacci (1170–1240) hatte auf Reisen nach Afrika, Byzanz und Syrien die arabische Mathematik kennengelernt. Nach ihm ist die Zahlen-Folge benannt, die wahrscheinlich schon in der griechischen Antike und in Indien bekannt war.

In der Fibonacci-Folge wird, ausgehend von der Summe aus 0 und 1, zu der Summe der jeweils zweite Summand addiert. Sie entsteht also folgendermaßen:
0+1=1,  1+1=2,  2+1=3,  3+2=5,  5+3=8,  8+5=13,  13+8=21, 21+13=34, 34+13=55 …
Auf diese Weise lässt sich die Fibonacci-Folge unendlich fortsetzen: siehe weiter unten.

Etwas überraschend: Die Quotienten zweier aufeinander folgender Fibonacci-Zahlen nähern sich, je weiter man in der Zahlenfolge fortschreitet, immer mehr dem rechnerischen Wert für den Goldenen Schnitt: 1,618033988…

Fibonacci-Folge (Anfang)
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

Die Quotienten-Folge wurde zur Übersichtlichkeit auf 4 Dezimal-Stellen begrenzt.
1,0000 2,0000 1,5000 1,6667 1,6000 1,6250 1,6154 1,6190 1,6176 1,6182 1,6180 1,6181 1,6180

Auch zur “Konstruktion” einer speziellen Spirale lässt sich die Fibonacci-Folge verwenden. Wegen des Zusammenhangs mit dem Goldenen Schnitt nennt man sie “Goldene Spirale”:

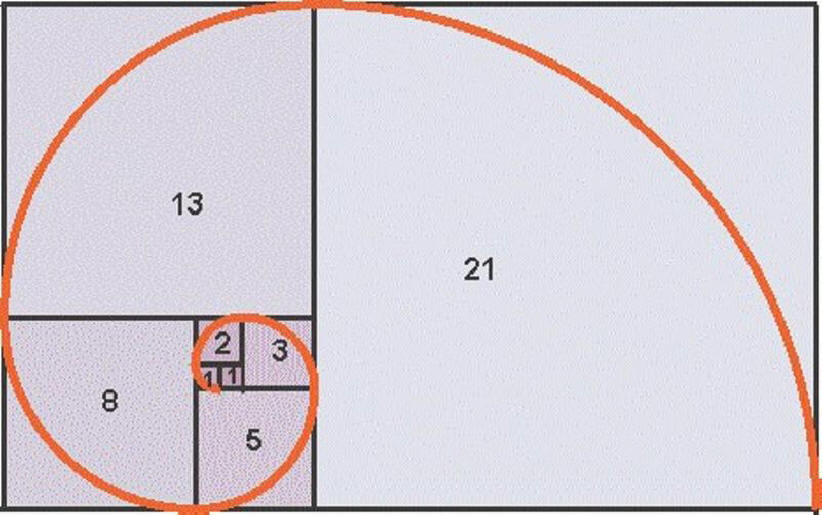
Diese “Goldene Spirale” kommt auch in der Natur vor – wir können sie an zwei von vielen Beispielen erahnen: an der Nautilus-Schnecke und am Sonnenblumen-Blütenkorb.
(Quelle beider Bilder: Internet)